Orbital Mechanics for Dummies - Circular Orbits

Last time we looked at the kinds of basic orbits, and gave a description of how the orbiting body moves in each.  Now we will dip our toe in the maths water.

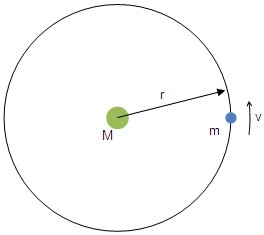
The first step is to define the parameters of the orbit, according to the following diagram.

M is the mass of the central body, in kilograms (kg).
m is the mass of the orbiting body, in kilograms (kg).
r is the orbital radius between the centres of the bodies, in metres (m).
v is the speed at which the orbiting body moves around the central body, in metres per second (m/s).

There are a few other parameters we'll use along the way:

G is Newton's gravitational constant, and is equal to 6.67 x10^-11 m³/kg/s².

V_C is the speed of a body moving in a perfect circular orbit, in metres per second (m/s).

V_E is the speed of a body moving just fast enough to escape from orbit, in metres per second (m/s).

A is an acceleration, expressed as a change in speed per second (m/s²).

From the previous post we know that for a circular orbit the orbiting body moves under centripetal acceleration which is provided by the gravity field of the central body.  So we need formulae for both centripetal acceleration and gravitational acceleration.

From high school physics we recall that centripetal acceleration is given by

A_C = V²/r

and gravitational acceleration is given by

A_G = GM/r²

Now since centripetal acceleration is provided by gravitational acceleration, A_C = A_G so

V²/r = GM/r²

and because we can eliminate the /r on each side, and in a circular orbit V = V_C

V_C² = GM/r  [1]

There we have it, our first equation for orbital mechanics.  Wasn't so hard, was it?   It's such an important equation that I've labelled it [1] so we can refer to it again.  What it tells us is that the square of the orbital speed is proportional to the mass of the central body, and inversely proportional to the orbital radius.  The constant of proportionality is Newton's gravitational constant.

Example

To try this out, let's work out how fast the International Space Station (ISS) travels around the Earth.  As I remember, it's around 17,500mph.  But can our equation [1] confirm that?

The mass of the Earth is 5.97 x10²⁴ kg.

The radius of the Earth is 6.37 x10⁶ m.

The ISS orbits at 350km above the surface, so the orbital radius is 6.72 x10⁶ m.

V_C² = GM/r = 6.67 x10^-11 x 5.97 x10²⁴ / 6.72 x10⁶ = 59.3 x10⁶.

Taking the square root gives

V_C =7,700 m/s.

Since there are 1,610 metres in a mile, and 3,600 seconds in an hour,

Orbital Speed = 7,700 x 3,600 / 1,610 = 17,200 mph.

That works for me!  Next time we'll take on the giant of orbital mechanics and prove Kepler's third law.